MA8251 Important 16 Mark questions ENGINEERING MATHEMATICS 2 Regulation 2017 Anna University free download. ENGINEERING MATHEMATICS 2 MA8251 Important 16 Mark questions pdf free download.
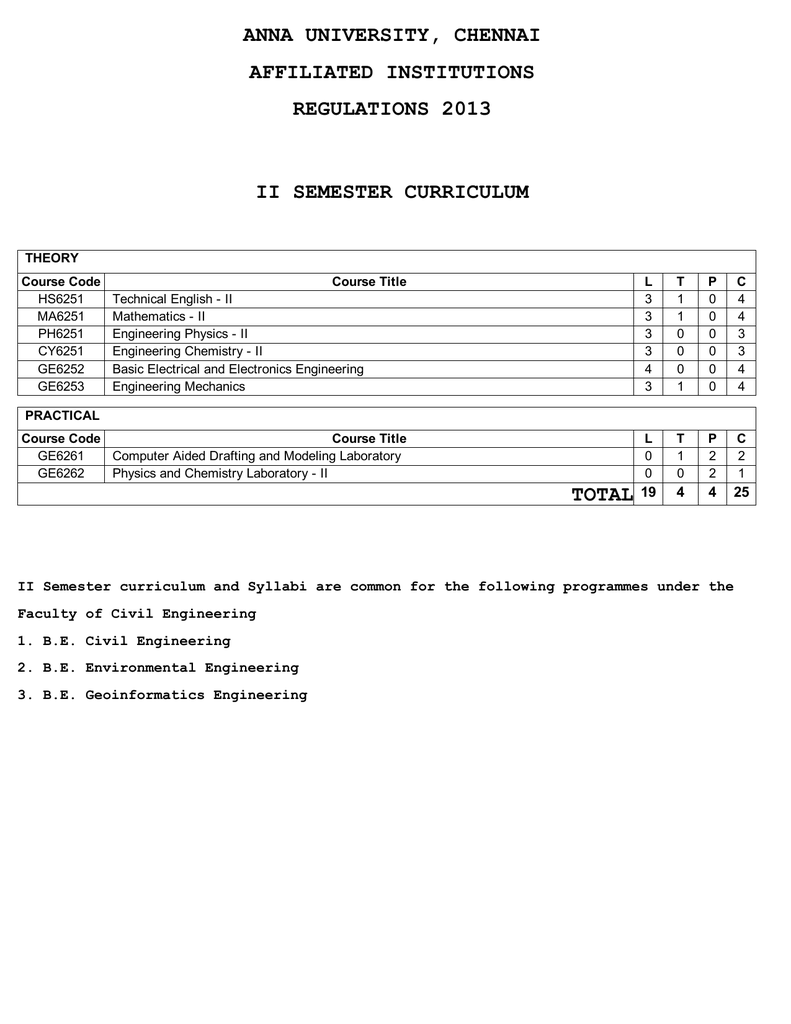

Sample MA8251 Important 16 Mark questions ENGINEERING MATHEMATICS 2:

. Online Objective Test for School Mathematics. Textbook Mathematics-II (Regulation 2017). Solution to Textbook Exercise Problems. Probability and Random Processes - Book. Statistics and Numerical Methods - Book. Numerical Methods - Book. Discrete Mathematics - Book. Textbook Mathematics-I (Regulation 2017). MA6251 – ENGINEERING MATHEMATICS – II SYLLABUS (REGULATION 2013) ANNA UNIVERSITY UNIT I: VECTOR CALCULUS (MA6251) Gradient, divergence and curl – TAKE THIS COURSE ₹ 499.00 ₹ 299.00 per 210 days.
- Reduce the quadratic form 8×2+7y2+3z2-12xy+4xz-8yz into canonical
form by orthogonal reduction and find its nature. - Calculate the angle between the normals to the surface 2 xy z at the
points (4,1,2) and(3,3,-3). (MA8251 Important 16 Mark questions Engineering Mathematics 2) - Find the value of n such that ??? is both solenoidal and irrotational
- Formulate the image of |? + ?| = ? under the map ? = ?/?. BTL
- Show that the transformation ? =
?
? maps, in general, circles and
straight lines into circles and straight lines. Point out the circles
and straight lines are transformed into straight lines and circles
respectively. (MA8251 Important 16 Mark questions Engineering Mathematics 2) - Solve the bilinear transformation that maps the point ?? = ?,
?? = −?, ?? = ?into the points ?? = ?, ?? = ?, ?? = ∞
respectively (MA8251 Important 16 Mark questions Engineering Mathematics 2) - Identify the bilinear transformation that maps ? + ?, −?,
? − ? at the z-plane into the points ?, ?, ? of the w-plane. - Identify the bilinear mapping which maps ?, ?, −? of the z-plane
onto ?, ?, ∞ of the w-plane. Show that the transformation maps the
interior of the unit circle of the z-plane onto the upper half of the
w-plane. - If ? = ???, ?? + ????, ?? is an analytic function , show that the
curves of the family ???, ?? = ? and the curves of the family
???, ?? = ?, cut orthogonally where ? and ? are varying
constants. (MA8251 Important 16 Mark questions Engineering Mathematics 2) - Identify the Laplace Transform of the function [? ????? ??? ??]
| Subject name | ENGINEERING MATHEMATICS 2 |
| Subject Code | MA8251 |
| Regulation | 2017 Regulation |
Engineering Mathematics 2 Notes
MA8251 Important 16 Mark questions ENGINEERING MATHEMATICS 2 Click here to download
